Uji T Satu Sampel dan Dua Sampel – Uji “t” atau Test “t” adalah salah satu test statistik yang dipergunakan untukmenguji kebenaran atau kepalsuan hipotesis nihil yang menyatakan bahwa diantara dua buah mean sampel yang diambil secara random dari populasi yang sama, tidak terdapat perbedaan yang signifikan.(Sudjiono, 2010:278).
Sebagai salah satu test statistik parametrik, Test “t” mula pertama dikembangkan oleh William Seely Gosset pada 1915. Pada waktu itu dia menggunakan nama samaran student, dan huruf “t” yang terdapat pada istilah Test “t” itu diambilkan huruf terakhir nama beliau. Itupun pula sebabnya mengapa Test “t”, sering disebut dengan nama atau istilah student t.
Pangkal tolak berpikir pada Test “t” secara singkat adalah sebagai mana tergambar pada uraian berikut.
Tujuan utama kegiatan penelitian antara lain adalah menemukan prinsip yang dapat diberlakukan secara umum atau bersifat universal. Untuk dapat mendapatkan prinsip yang berlaku universal itu, secara ideal teoritis, seorang peneliti harusnya meneliti keseluruhan objek yang dia hadapi, dengan kata lain: meneliti populasinya. Dengan meneliti populasinya, generalisasi yang dikemukakan oleh seorang peneliti tidak akan jauh berbeda dengan kenyataan yang sebenarnya. Akan tetapi kenyataan menunjukkan, meneliti populasi secara keseluruhandalam rangka membuat generalisasi itu, kecuali tidak mungkin, juga tidak praktis, sebab kenyataan acapkali menunjukkan sangat besar atau sangat luas populasi itu. Itulah sebabnya mengapa sebelum dilakukan pengukuran, populasi itu perlu “diubah” terlebih dahulu kedalam populasi yang lebih kecil yang kemudian kita kenal dengan istilah sampel.
Uji t Satu Sampel
Uji t Satu sampel digunakan untuk menguji perbedaan rata-rata suatu variabel dengan suatu konstanta tertentu atau nilai hipotesis.
Contoh, Produsen tabung gas menyatakan berat tabung gas adalah 15Kg. Untuk mengetahui kebenarannya maka dilakukan sampling. Data yang diperoleh adalah sebagai berikut.

![]()
Data Berat Tabung
Analisis Uji t satu sampel dilakukan dengan langkah-langkah sebagai berikut:
- Klik Analyze => Compare Means => One-Sample T Test kemudian akan muncul kotak dialog seperti dibawah ini
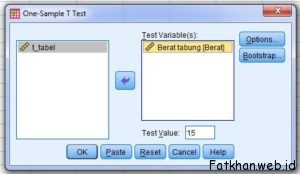
Kotak Dialog One-Sample T Test
- Masukkan variabel Berat tabung pada kotak Test Variabel(s) dan masukkan 15 pada kotak Test Value.
- Klik options sehingga kotak dialog One-Sample T Test; Option, tingkat kepercayaan dan Missing Values muncul. Secara default tingkat kepercayaan 95% dan Missing Values – Exclude cases analysis by analysis yang berarti hanya data yang valid yang digunakan dalam analisis.
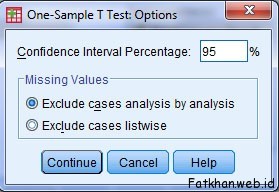
Kotak Dialog One-Samples T Test: Options
- Klik Continue sehingga kembali ke kota dialog One-Sample T Test.
- Klik OK sehingga akan muncul Output SPSS sebagai berikut:

Tabel One-Sample Statistic memaparkan nilai statistik variabel berat tabung sebagai berikut: jumlah sampling 20, rata-rata berat tabung 14,99 kg, standar deviasi 0,35079 kg dan Std.Error Mean 0,07844 kg.

Sebelum kita membahas uji hipotesis, perlu terlebih dahulu diketahui aturan dasar yang menyertai. Uji hipotesis pada dasarnya adalah membandingkan nilai t atau f hitung dengan t atau f tabel. Aturannya adalah sebagai berikut;

Ho =Rata-rata berat tabung 15 kg.
H1 =Rata-rata berat tabung ≠ 15 kg.
Nilai t hitung -0.127, Mutlaknya 0.127.
T hitung (0.127) < t tabel (19;0.025) adalah 2.093, maka Ho diterima. Jadi tidak ada perbedaan rata-rata berat tabung.
Maksud t tabel (19;0.025) adalah df = 19 dari jumlah sampel 20 dikurangi 1. Uji adalah dua sisi. Jadi setiap sisinya memiliki nilai setengah α. Bila dipakai
- = 0.05 maka setengah α adalah 0.025. Untuk mencari nilai t tabel (19;0.025) gunakan fungsi idf.T pada SPSS. Pada NumericExpression ID.T(?.?) ganti tanda tanya dengan nilai sebagai beri kut: IDF.T (0.975,19). Milai 0.975 berasal dari 100% atau 1 dikurangi 0.025 dan 19 adalah nilai df.
Disamping menggunakan perbandingan t hitung dan t tabel,anda dapat melakukan perbandingan Sig(2-tailed) dengan α.
Sig(2-tailed) (0.900) > α (0.025), maka Ho diterima.
Dependen Sample t Test
Dependen Sample t Test adalah analisis pengukuran pada subjek yang sama terhadap suatu pengaruh atau perlakuan tertentu. Pengukuran pertama dilakukan sebelum diberi perlakuan tertentu pengukuran kedua dilakukan setelah dilakukan sesudahnya. (Trihendradi, 2010:117).
Contoh pada penelitian perbedaan nilai TOEFL sebelum dan sesudah mengikuti test intensif selama 1 bulan. Berikut datanya:
A | B | A | B | A | B |
350 | 400 | 375 | 500 | 300 | 425 |
325 | 400 | 325 | 450 | 350 | 475 |
375 | 475 | 300 | 425 | 375 | 500 |
350 | 500 | 325 | 400 | 300 | 375 |
325 | 425 | 350 | 475 | 325 | 450 |
375 | 500 | 375 | 525 | 325 | 400 |
350 | 450 | 325 | 450 | 375 | 450 |
325 | 400 | 350 | 425 | 300 | 375 |
300 | 400 | 350 | 400 | 350 | 425 |
350 | 475 | 325 | 425 | 375 | 525 |
Data Pasangan Nilai TOEFL
Langkah selanjutnya adalah melakukan Independen samples t test pada SPSS sebagai berikut:
- Pilih Analyza => Compare Means => Paired Sample T Test maka akan muncul kotak dialog seperti di bawah ini.
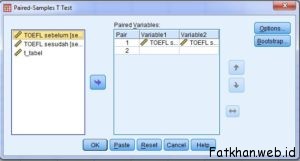
Kotak Dialog Paired Sample t Test
Blok variabel TOEFL sebelum dan sesudah kemudia masukkan pada kotak Paired Variables. Setelah itu klik OK. Kemudian akan muncul output dari SPSS sebagai berikut:
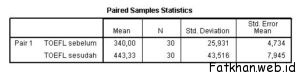
Tabel diatas menggambarkan pasangan nilai TOEFL. Nilai rata-rata sebelum pelatihan intensif adalah 340, sedangkan setelah pelatihan 443.33. Jumlah pasangan sampel ada 30. Standar deviasi sebelum pelatihan intensif adalah 25.931 dan setelah pelatihan adalah 43.516. Standard error sebelum pelatihan adalah 4.734, sedangkan setelah pelatihan 7.945.
Tabel kedua yaitu tabel Paired Samples Correlation. Tabel ini menunjukkan tingkat hubungan variabel sebelum pelatihan dengan variabel sesudah pelatihan. Nilai korelasinya adalah (0.760). nilai tersebut mengindikasikan hubungan erat.

Tabel ketiga, Paired Samples Test, memuat uji t dan interval keyakinan. Ada perbedaan rata-rata sebelum dan sesudah pelatihan sebesar 103.33, dengan nilai standar deviasi 29.165 dan standard error 5.325. Signifikankah perbedaan tersebut?
Apabila melihat kolom 95% convidence interval, terlihat batas bawahnya adalah -114.224 sedangkan atasnya adalah -92.443. Nilai perbedaan pasangan -103.333 berada pada rentang tersebut. Untuk kepastiannya, lihat t testnya.

Nilai t hitung adalah -19.405 dan df = 29 maka diperoleh Sig (2-tailed) atau p-value sebesar 0. Nilai p-value tersebut lebih kecil dibandingkan dengan level alfa (0.025). Maka dapat disimpulkan ada perbedaan rata-rata nilai TOEFL sebelum dan sesudah mengikuti test intensif.
Independen Sample t Test
Independen Sample t Test digunakan untuk menguji signifikansi beda rata-rata dua kelompok. Sebagai contoh penelitian tingkat kecerdasan antara remaja putra dan putri, berikut datanya:

Data Tingkat Kecerdasan
Sebelum melakukan analisis Independen Sample t Test, terlebih dahulu harus memberikan bobot pada variabel jumlah. Langkahnya sebagai berikut;
- Klik Data => Weight Cases pada menu hingga kotak dialog Weight Cases muncul.
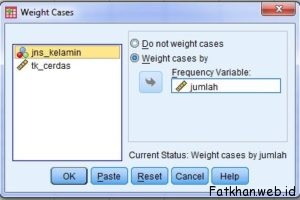
Kotak Dialog Weight Cases
- Pilih Weight Cases by, pada kotak Frequency Variabel, masukkan variabel jumlah.
- Klik OK.
Langkah selanjutnya melakukan analisis Independent sample t Test, langkahnya sebagai berikut:
- Klik Analyze => Compare Means => Independen Sample T Test, dan akan muncul kotak dialog seperti di bawah ini.
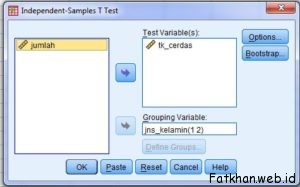
Kotak Dialog Independen Samples-T Test.
- Masukkan variabel tk_cerdas pada kotak Test variabel(s) dan masukkan variabel jns_kelamin pada kotak Grouping Variable.
- Klik Define Group, masukkan nilai variabel jns_kelamin pada kotak Group 1 dan 2.

Kotak Dialog Define Group.
- Klik Continue sehingga akan kembali ke kotak Independen-Sample T Test.
- Klik Options sehingga kotak dialog Independen Sample T Test; Option muncul. Secara default tinggak kepercayaan 95% dan Exclude cases analysis by analysis.
- Klik Continue, kemudian klik OK, kemudian muncul Output hasil analisis SPSS sebagai berikut:
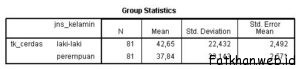
Tabel group statistik memaparkan jumlah data/sampel, niai rata-rata, dan standard deviasi. Rata-rata tingkat kecerdasan laki-laki (42.65) lebih kecil dibanding perempuan (23.143).

Tabel Independen Sample Test yang pertama menguji apakah kedua kelompok memiliki varian yang sama.
Ho = Kedua kelompok memiliki varian yang sama.
H1 = Kedua kelompok tidak memiliki varian yangs sama.
Nilai Sig (0.628) > α (0.05), maka Ho diterima. Jadi kedua kelompok memiliki varian yang sama.
Tabel Independen Sample Test yang kedua menguji apakah kedua kelompok memiliki rata-rata yang sama.
Ho = Kedua kelompok memiliki rata-rata tingkat kecerdasan yang sama.
H1 =Kedua kelompok tidak memiliki rata-rata tingkat kecerdasan yang sama.
T hitung (1.345) < t tabel (80;0.025) adalah 1.990, maka Ho diterima. Jadi kedua kelompok memiliki tingkat rata-rata kecerdasan yang sama. Dengan kata lain tidak ada perbedaan rata-rata tingkat kecerdasan antara siswa perempuan dan siswa laki-laki.
Disamping menggunakan perbandingan t hitung dengant tabel, dapat juga dilakukan perbandingan Sig (2-tailed) dengan α.
Sig(2-tailed) (0.181) > α (0.025), sehingga Ho diterima.
Demikian penjelasan tentang Uji T Satu Sampel dan Dua Sampel semoga bermanfaat dan dapat dijadikan referensi, jika artikel ini bermanfaat bai anda silahkan share artikel ini. Terima kasih

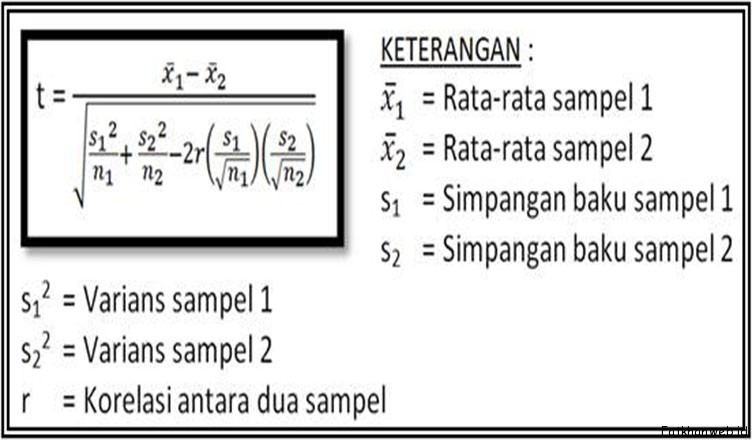











“Tabel group statistik memaparkan jumlah data/sampel, niai rata-rata, dan standard deviasi. Rata-rata tingkat kecerdasan laki-laki (42.65) lebih kecil dibanding perempuan (23.143).”
bukankah seharusnya
“Tabel group statistik memaparkan jumlah data/sampel, niai rata-rata, dan standard deviasi. Rata-rata tingkat kecerdasan laki-laki (42.65) lebih BESAR dibanding perempuan (37.84).”