Teknik Analisis Data Untuk Penulisan Karya Ilmiah

Berikut ini adalah teknik analisis data untuk penulisan ilmiah,

Type Data :

1. Data Nominal (non-par), (Data Kategorikal)

2. Data Ordinal (non-par), (Data Numerikal (Diskrit – Kontinue))

3. Data Interval (par)

4. Data Ratio (par)

Analisis Data :

1. Analisis Deskriptif (Tabulasi, Grafik)
   Data Kategorial     : Bar chart, Pie Chart, Pareto.
   Data Numerik       : Grafik line, Scater diagram, order ray, Steam and Leaf, tabel kontingensi
2. Analisis Inferen (Uji normalitas dan linieritas, Uji validitas dan reliabilitas, Uji perbedaan, Uji hubungan, lainnya)
3. Kombinasi Dari Keduanya

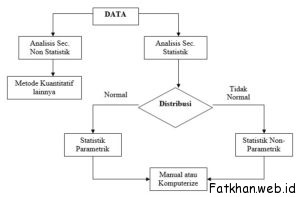
STATISTIK DESKRIPTIF

• Data Kategorial : Bar chart, Pie Chart, Pareto.
• Data Numerik : Grafik line, Scater diagram, order ray, Steam and Leaf, tabel kontingensi

KORELASI

2. Data Nominal dan Ordinal , digunakan :

    

   • Contingency coeficient
   • Phi & Cramer’s V
   • Lambda
   • Gamma
   • Sommer’s d
   • Kendall
   • Spearman

2. Data Interval dan Rasio

    

   •  Pearson

CROSSTAB

Analisis :

Ho : Tidak ada hubungan antara variable baris dengan variable kolom

H1 : Ada hubungan antara variable baris dengan variable kolom.

Dasar Pengambilan Keputusan :

1.    Berdasarkan perbandingan uji chi kuadrat dan table

Jika chi kuadrat  Uji >  chi kuadrat  table Ho diterima

     2.   Berdasarkan nilai  probabilitas

      Tentukan nilai alfa

• Jika nilai probabilitas/sigf. > alfa , Ho diterima
• Jika nilai probabilitas/sigf. < alfa, Ho ditolak

A. UJI NORMALITAS

1. RASIO SKEWNESS  DAN  RASIO KURTOSIS

            Rasio Skewnwss = Nilai Skewnwss / S.E. Skewness

            Rasio Kurtosis = Nilai Kurtosis / S.E. Kurtosis

            Jika Nilai Rasio Diantara   – 2 s/d + 2 à Sebarannya Bersifat Normal

2. UJI KOLMOGOROV SMIRNOV  = UJI LILLIEFOR

            Jika Nilai Prob. / Sig F > 5 % à Sebaran Bersifat Normal

            Jika Nilai Prob. / Sig F < 5 % à Sebaran Bersifat Tidak Normal

3. UJI SHAPIRO WILK

            Jika Nilai Prob. / Sig F > 5 % à Sebaran Bersifat  Normal

            Jika Nilai Prob. / Sig F < 5 % à Sebaran Bersifat Tidak Normal

4. GAMBAR / PLOT

            Histogram dengan Normal Curve

            Q-Q Plot

            Pembentukan Garis Berdasarkan Nilai Z.

            Jika Data Tersebar Di sekeliling Garis à Berdistribusi Normal

5. DETRENDED Q-Q PLOT

Pembentukan Garis Untuk Mendeteksi Pola-pola Dari  Titik-titik Yang Bukan bagian datri normal.

            Jika Data Tersebar Di Sekeliling Garis àBerdistribusi Normal

B. UJI   LINIERITAS

Uji Linieritas Hanya Digunakan Untuk Uji Sebab Akibat (Uji Pengaruh)

1. MENGGUNAKAN UJI REGRESI

            Nilai Sig F  Dari Uji F

            Jika Nilai Sig F < 5 %, Model Linearitas Dapat Dignakan

            Jika Nilai Sig F > 5 %, Model Linearitas Tidak Dapat Digunakan

2. MENGGUNAKAN SCATTER PLOT

            Scatter Plot Yang Menunjukkan Hubungan Yang Linear, Terlihat Dari Titik Yang Mengumpul Di Suatu Garis.

C. UJI HOMOGENITAS

Uji Homogenitas Digunakan Untuk Uji Beda

Uji Homogenitas Menggunakan Uji Levene

• Jika Nilai Sig < 5 %, Data Berasal Dari Populasi-Populasi Yang Mempunyai Varians Yang Tidak Sama.
• Jika Nilai Sig > 5 %, Data Berasal Dari Populasi-Populasi Yang Mempunyai varian yang sama

UJI PHI, CRAMER’S V, CONTINGENCY COEFISIENT

• Untuk uji hubungan variable yang bersifat nominal dan hubungan ke dua  variabel adalah simetris

• Kesimpulan yang dihasilkan : Ada / tidaknya hubungan, dengan memperhatikan nilai sig.
• Besar korelasi antar variable

          Hubungan erat jika value mendekati 1

          Hubungan lemah jika value mendekati 0

UJI LAMBDA

•  Untuk uji hubungan variable yang bersifat nominal dan hubungan ke dua variabel adalah Directional Measures

•  Directional Measures digunakan jika salah satu variable merupakan var.  dependen , sedangkan variable lainnya akan menjadi variable independen.

UJI GAMMA, KENDALL’S TAU, SOMERS’D

•  Untuk uji hubungan variable yang bersifat ordinal.
•  Besarnya korelasi antar variable ditentukan jika :

            Value bernilai  mendekati +1 atau –1 à hub. Kuat

            Value bernilai mendekati 0 bernilai lemah.

    Tanda + atau – àmenyatakan sifat hubungan

UJI BEDA

MACAM UJI BEDA :

1. UJI BEDA RATA-RATA 2 POPULASI

            POPULASI INDEPENDENT

                        POPULASI DGN VARIAN SAMA

                        POPULASI DGN VARIAN BEDA

            POPULASI PAIR

                        POPULASI DGN VARIAN SAMA

                        POPULASI DGN VARIAN BEDA

ANALISISNYA MENGGUNAKAN UJI T

2. UJI BEDA RATA-RATA  > 2 POPULASI

UJI BEDA DENGAN 1 PERLAKUAN

UJI BEDA DENGAN 2 PERLAKUAN

ANALISISNYA MENGGUNAKAN UJI ANOVA

PERBANDINGAN METODE PENGUJIAN DENGAN MENGGUNAKAN PARAMETRIK ATAU NON-PARAMETRIK

UJI BINOMIAL

UNTUK KASUS DIKOTOMI

JIKA TIDAK DIKOTOMI, GUNAKAN CUTPOINT

Ho : frekuensi observasi kategori I = frekuensi observasi kategori II

H1 : frekuensi observasi kategori I ¹ frekuensi observasi kategori II

Jika ada perbandingan tertentu yang ingin dilihat, gunakan TEST PROPORTION sesuai yang diinginkan.

UJI CHI-KUADRAT

UNTUK KASUS YANG TIDAK DIKOTOMI

Pembentukan Hipotesis pada uji chi-kuadrat :

Ho : proporsi seluruh kategori bernilai sama

H1 : ada proporsi dari kategori yang dibandingkan bernilai tidak sama

Atau

Ho : proporsi kategori yang ada sama dengan nilai yang telah ditentukan

H1 : proporsi kategori yang ada tidak sama dengan nilai yang telah ditentukan.

UJI KOLMOGOROV SMIRNOV

Ho: Data dapat diasumsikan berdistribusi uniform, normal, poisson

H1: Data tidak dapat diasumsikan berdistribusi uniform, normal, poisson.

UJI MANN-WHITNEY, UJI KS, UJI RUN WW, UJI MOSES

Ho : dua sampel independen berasal dari populasi yang identik atau dari populasi  yang mempunyai mean yang sama.

H1 : dua sampel independen berasal dari populasi yang berbeda atau dari populasi yang mempunyai mean yang beda.

UJI TANDA, UJI WILCOXON,  UJI MCNEMAR

Ho : Tidak terdapat perbedaan sebelum dan sesudah perlakuan

H1 : Terdapat perbedaan sebelum dan sesudah perlakuan.

UJI KRUSKAL W., UJI MEDIAN

Ho : Populasi yang dibandingkan mempunyai nilai rata2 yang sama

H1 : Tidak semua populasi mempunyai nilai rata2 yang sama.

UJI FRIEDMAN, UJI W.KENDALL, UJI Q-COCHRAN

Ho : K perlakuan yang dibandingkan adalah sama

H1 : ada K perlakuan yang dibandingkan yang tidak sama.

Referensi

Cooper., Donald R. and chindler., Pamela S. 2003. Business Research Methods. Boston: International edition. Mc Graw Hill;

Husen Umar. 1999. Riset Akuntansi. Jakarta:

Kerlinger., Fred N. 2002. Foundation of Behavioral Research. 3th Ed. New Jersey: Holt, Rinehart and Winston Publishing Co.;

Moh. Nasir.1999. uMetode Penelitian. Cetakan keempat. Jakarta:    Ghalia Indonesia;

Sekaran., Uma. 2003. Research Methods For Business. Fourth Edition. New          York: John Willey & Sons, Inc.