Pengertian Dan Contoh Kasus Uji Regresi Linear Sederhana Dan Berganda

Pengertian Dan Contoh Kasus Uji Regresi Linear Sederhana Dan Berganda – Regresi merupakan suatu alat ukur yang juga digunakan untuk mengukur ada atau tidaknya korelasi antarvariabel. Istilahregresi yang berarti ramalan atau taksiran pertama kali diperkenalkan oleh Sir Francis Galton pada tahun 1877.

Analisis regresi adalah studi tentang masalah hubungan beberapa variabel yang ditampilkan dalam persamaan matematika (Andi, 2009). Analisis regresi lebih akurat dalam melakukan analisis korelasi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula karena pada analisis ini kesulitan dalam menunjukkan slop (tingkat perubahan suatu variabel terhadap variabel lain dapat ditentukan).

Analisis regresi terbagi menjadi dua yaitu regresi linier dan Nonlinier. Analisi regresi linear terdiri dari analisis regresi linear sederhana dan analisis regresi linear berganda. Perbedaan antar keduanya terletak pada jumlah variabel independennya. Regresi linear sederhana hanya memiliki satu variabel independen, sedangkan regresi linear berganda mempunyai banyak variabel independen. Analisis regresi Nonlinier adalah regresi eksponensial.

KRITERIA DATA REGRESI LINIER

Terdapat dua syarat yang harus dipenuhi oleh data dalam menggunakan analisis regresi linier yaitu:

1. Data

Data harus terdiri dari dua jenis variabel, yaitu dependen dan independen. Selain itu data berupa kuantitatif fan variabel berupa kategori, seperti SD, SMA, SMK, dll.

2. Asumsi

Setiap data diasumsikan variabel dependen terdistribusi secara normal. Selain itu, antara variabel dependen dan independen harus memiliki hubungan linier dengan observasi harus saling bebas.

REGRESI LINEAR SEDERHANA

Regresi linear sederhana adalah hubungan secara linear antara satu variabel independen (X) dengan variabel dependen (Y). Analisis ini digunakan untuk mengetahui arah hubungan antara variabel independen dengan variabel dependen apakah positif atau negatif serta untuk memprediksi nilai dari variabel dependen apabila nilai variabel independen mengalami kenaikan atau penurunan nilai. Data yang digunakan biasanya berskala interval atau rasio.

Rumus dari dari analisis regresi linear sederhana adalah sebagai berikut:

Y’ = a + bX

Keterangan:

Y= subyek dalam variabel dependen yang diprediksi

a = harga Y ketika harga X= 0 (harga konstan)

b = angka arah atau koefisien regresi, yang menunjukkan angka peningkatan ataupun penurunan variabel dependen yang didasarkan pada perubahan variabel independen. Bila (+) arah garis naik, dan bila (-) maka arah garis turun.

X = subyek pada variabel independen yang mempunyai nilai tertentu.

Secara teknik harga b merupakan tangent dari perbandingan antara panjang garis variabel dependen, setelah persamaan regresi ditemukan.

Dimana :

R  = koefisien korelasi product moment antara variabel variabel X dengan variabel Y

S_y = simpangan baku variabel Y

S_x = simpangan baku variabel X

Jika harga b merupakan fungsi dari koefisien korelasi. Bila koefisien korelasi tinggi, maka harga b juga besar, sebaliknya bila koefisien korelasi rendah maka harga b juga rendah (kecil). Selain itu bila koefisien korelasi negatif maka harga b juga negatif, dan sebaliknya bila koefisien korelasi positif maka harga b juga positif.

Selain itu harga a dan b dapat dicari dengan rumus berikut:

Uji Koefisien Regresi Sederhana (Uji t)

Uji ini digunakan untuk mengetahui apakah variabel independen (X) berpengaruh secara signifikan terhadap variabel dependen (Y). Signifikan berarti pengaruh yang terjadi dapat berlaku untuk populasi (dapat digeneralisasikan).

Rumus t hitung pada analisis regresi adalah sebagai berikut:

Langkah-langkah pengujian koefisien regresi sederhana adalah sebagai berikut:

1. Menentukan Hipotesis

H_o = Tidak ada pengaruh yang signifikan

H_{a =} ada pengaruh yang signifikan

2. Menentukan tingkat signifikansi

Biasanya menggunakan a = 5% atau 0,05

3. Menentukan t hitung
4. Menentukan t tabel
5. Membandingkan t hitung dan t table dengan kriteria

H_o diterima jika: t hitung ≥ t tabel
H_o ditolak jika: t hitung < t tabel
H_o diterima jika: -t hitung ≤ t tabel
H_o di tolak jika: -t hitung > t tabel

Contoh Kasus

Seorang pengusaha bernama Andrianto ingin meneliti tentang pengaruh biaya promosi terhadap volume penjualan pada perusahaan minyak wangi. Dari pernyataan tersebut didapatvariabel dependen (Y) adalah volume penjualan dan variabel independen (X) adalah biaya promosi. Data-data yang didapat ditabulasikan sebagai berikut:

Langkah :

• Buka file : korelasi & regresi
• Klik Analyze, klik Regression, dan klik linier
• Klik dan pindahkan volume penjualan ke kotak dependent dan biaya promosi ke kotak independent dengan mengetik tanda ►
• Klik statistics pilih estimates, model fit, dan descriptive.
• Klik continue
• Klik plots
• Pada standardized residual plots, pilih histogram dan normal probability plot.
• Klik continue dan klik OK.

Output pada SPSS dapat dilihat sebagai berikut:

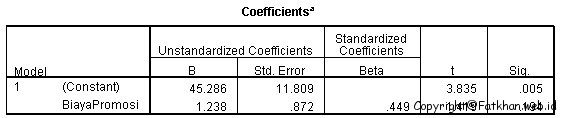
Dari hasil perhitungan didapatkan:

Y= a + bx

Konstanta (a) = 45.286; Koefisien Regresi (b) = 1,238; dan t hitung = 1.419

Selanjutnya yaitu menganalisis signifikansi pengaruh variabel independen dengan variabel dependen. Jika ditetapkan hipotesis sebagai berikut:

8. Tidak ada pengaruh secara signifikan antara biaya promosi dengan volume penjualan
8. Ada pengaruh signifikan antara biaya promosi dengan volume penjualan

Dengan menggunakan tingkat signifikansi 5%, pengujian 2 sisi, dan derajat kebebasan (df) = n-k-1 = 10-1-1 = 8 (dimana n = jumlah data, k = jumlah variabel independen) maka diperoleh t tabel sebesar 2.30600. (dapat dilihat pada Ms Excel dengan mengetikkan “=tinv(0,05;8)” lalu tekan Enter).

Karena t hitung < t tabel, maka Ha diterima. Kesimpulannya, terdapat pengaruh yang signifikan antara biaya promosi dengan volume penjualan.

Kasus kedua

Seorang guru yang bernama IDNAS secara tidak sengaja mencari tahu hubungan antara uang saku dengan nilai siswa. Dari pernyataan tersebut didapat  variabel dependen (Y) adalah nilai siswa dan variabel independen (X) adalah Uang saku. Data-data yang didapat ditabulasikan sebagai berikut:

Langkah :

• Buka file : korelasi & regresi
• Klik Analyze, klik Regression, dan klik linier
• Klik dan pindahkan nilai siswa ke kotak dependent dan uang saku ke kotak independent dengan mengetik tanda ►
• Klik statistics pilih estimates, model fit, dan descriptive.
• Klik continue
• Klik plots
• Pada standardized residual plots, pilih histogram dan normal probability plot.
• Klik continue dan klik OK.

Output pada SPSS dapat dilihat sebagai berikut:

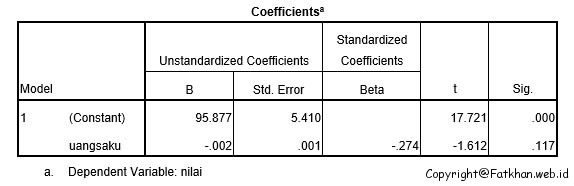
Dari hasil perhitungan didapatkan:

Konstanta (a) = 95.877; Koefisien Regresi (b) = -0.002; dan t hitung = -1.612

Selanjutnya yaitu menganalisis signifikansi pengaruh variabel independen dengan variabel dependen. Jika ditetapkan hipotesis sebagai berikut:

H_o = Tidak ada pengaruh secara signifikan antara uang saku dengan nilai siswa

H_a = Ada pengaruh signifikan uang saku dengan nilai siswa.

Dengan menggunakan tingkat signifikansi 5%, pengujian 2 sisi, dan derajat kebebasan (df) = n-k-1 = 34-1-1 = 32 (dimana n = jumlah data, k = jumlah variabel independen) maka diperoleh t tabel sebesar 2.03693. (dapat dilihat pada Ms Excel dengan mengetikkan “=tinv(0,05;32)” lalu tekan Enter).

Karena -t hitung ≤ t tabel, maka H_o diterima. Kesimpulannya, tidak ada pengaruh yang signifikan antara uang saku dengan nilai siswa.

REGRESI LINEAR BERGANDA

Regresi linear berganda adalah hubungan secara linear antara dua atau lebih variabel independen (X₁, X₂, … X_n) dengan variabel dependen (Y). Analisis ini digunakan untuk mengetahui arah hubungan antara variabel independen dengan variabel dependen apakah masing-masing variabel independen berhubungan positif atau negatif dan untuk memprediksi nilai dari variabel dependen apabila nilai variabel independen mengalami kenaikan atau penurunan. Data yang digunakan biasanya berskala interval atau rasio.

Analisis regresi ganda digunakan oleh peneliti, bila peneliti bermaksud meramalkan bagaimana keadaan (naik turunnya) variabel independen (kriterium), bila dua atau lebih variabel independen sebagai faktor predictor dimanipulasi (dinaik turunkan nilainya). Jadi analisis regresi ganda akan dilakukan bila jumlah variabel independennya minimal 2.

Rumus dari analisis regresi linear berganda adalah sebagai berikut:

Analisis Korelasi Ganda (R)

Analisis ini digunakan untuk mengetahui hubungan antara 2 atau lebih variabel independen terhadap variabel dependen secara serentak. Nilai R berkisar antara 0 dan 1. Semakin mendekati angka 1 maka hubungan semakin kuat, sebaliknya jika semakin mendekati angka 0 maka hubungan semakin lemah.

Rumus korelasi ganda dengan 2 variabel independen adalah sebagai berikut:

Menurut Sugiyono (2007) pedoman untuk memberikan interpretasi koefisien korelasi adalah sebagai berikut:

Analisis Determinasi (R²)

Analisis ini digunakan untuk mengetahui presentase sumbangan pengaruh variabel independen secara serentak terhadap variabel dependen. Jika R² bernilai 0 maka tidak ada sedikitpun presentase sumbangan pengaruh yang diberikan variabel independen terhadap variabel dependen, tetapi jika R² bernilai 1 maka sumbangan pengaruh yang diberikan variabel independen terhadap variabel dependen adalah sempurna.

Rumus untuk mencari koefisien determinasi dengan 2 variabel independen adalah sebagai berikut:

Uji Koefisien Regresi Secara Bersama-sama (Uji F)

Uji ini digunakan untuk mengetahui apakah variabel independen secara bersama-sama berpengaruh secara signifikan terhadap variabel dependen, atau digunakan untuk mengetahui apakah model regresi dapat digunakan untuk memprediksi variabel dependen atau tidak. Signifikan berarti hubungan yang terjadi dapat berlaku untuk populasi (dapat digeneralisasikan).

Rumus untuk mencari F hitung adalah sebagai berikut:

Langkah-langkah dalam pengujian koefisien regresi secara bersama-sama adalah sebagai berikut:

• Merumuskan hipotesis

H_{o =}  Tidak ada pengaruh yang signifikan
H_{a =}  Terdapat pengaruh yang signifikan

      b. Menentukan tingkat signifikansi

Biasanya menggunakan taraf a = 5%

3. Menentukan F hitung
4. Menentukan F tabel

Dapat dicari dengan Ms. Excel menggunakan rumus “=finv(a,df1,df2)”

df1 = jumlah variabel independen

df2 = n-k-1

5. Membandingkan F hitung dan F tabel dengan kriteria

H_o = diterima jika: F hitung ≤ F tabel
H_a = ditolak jika: F hitung > F tabel

1. Uji Koefisien Regresi Secara Parsial (Uji t)

Uji ini digunakan untuk mengetahui apakah dalam model regresi variabel independen secara parsial berpengaruh signifikan terhadap variabel dependen.

Rumus t hitung pada analisis regresi ini adalah sebagai berikut:

Langkah-langkah pengujian koefisien regresi parsial adalah sebagai berikut:

1. Menentukan Hipotesis

H_a =  Secara parsial tidak ada pengaruh signifikan
H_o = Secara parsial terdapat pengaruh signifikan

       b. Menentukan tingkat signifikansi

Biasanya menggunakan taraf a = 5%

3. Menentukan t hitung
4. Menentukan t tabel

Dapat dicari dengan Ms. Excell menggunakan rumus “=tinv(a,df)” df = n-k-1

5. Membandingkan t hitung dan t tabel dengan kriteria

H_a = diterima jika: -t tabel ≤ t hitung < t table

H_o = ditolak jika: -t hitung < -t tabel atau t hitung > t table

Contoh Kasus

Seorang pengamat pasar modal bernama Sugianto ingin melakukan penelitian tentang faktor-faktor yang mempengaruhi harga saham pada perusahaan. Sugianto ingin mengetahui hubungan antara rasio keuangan PER dan ROI (Return On Investment) terhadap harga saham. Dari pernyataan tersebut, didapatkan variabel dependen (Y) yaitu harga saham, dan variabel independen (X₁ dan X₂) yaitu PER dan ROI. Data yang ditabulasikan sebagai berikut:

Langkah:

• Klik analyze, klik regression, klik linier
• Klik PER dan ROI dan masukkan ke kotak Independent
• Klik Harga Saham dan masukkan ke kotak Dependent.
• Klik statistic: pilih estimates, Model Fit, Descriptives
• Klik continue
• Klik Plots pada Standardized Residual Plot, pilih Histogram dan Normal Probability
• Klik Continue dan Klik OK

Output pada SPSS dapat dilihat sebagai berikut:

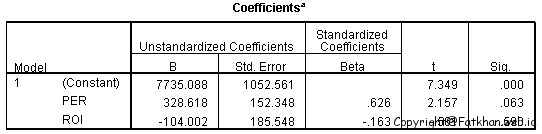
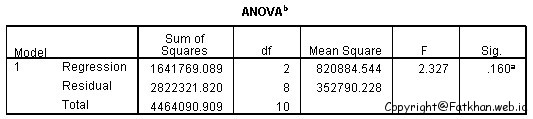
Dari hasil perhitungan diperoleh:

Konstanta (a) = 7735,088; Koefisien Regresi 1 (b1) = 328,618; Koefisien Regresi 2 (b2) = -104,002; R = 0,606; R² = 0,368; F hitung = 2,327; t hitung PER = 2,157 dan t hitung ROI = -0,561;

Kemudian kita hitung hasil analisis:

1. Analisis Korelasi Ganda (R)

R = 0,606 berdasarkan tabel Sugiyono (2007) hubungan antar variabel kuat

2. Analisis Determinasi (R²)
   R² = 0,368 jadi presentasi sumbangan pengaruh variabel sebesar 36,8 %
3. Uji Koefisien Regresi Bersama-sama (Uji F)

F hitung = 2,327

a = 5% = 0,05

df1 = 2 dan df2 = n-k-1 = 10-2-1 = 7

F tabel = finv(0,05;2;7) = 4,737

Karena F hitung ≤ F tabel, maka H_o diterima

4. Uji Koefisien Regresi Parsial (Uji t)

t hitung PER = 2,157 dan t hitung ROI = -0,561

a = 5% = 0,05

df = n-k-1 = 10-2-1 = 7

t tabel = tinv(0,05;7) = 2,364

Karena t hitung PER ≤ t tabel, maka H_o PER diterima

Karena t hitung ROI ≥ -t tabel, maka H_o ROI diterima

DAFTAR RUJUKAN

Andi. 2009. SPSS17 untuk Pengolah Data Statistik. Semarang:Wahana Komputer

Hasan M. Iqbal, Ir., M.M. 2005. Pokok-Pokok Materi Statistik 1 (Statistik Deskriptif). Edisi Kedua. Jakarta: PT. Bumi Aksara.

Priyatno Duwi. 2008. Mandiri Belajar SPSS (Statistical Product and Service Solution) Untuk Analisis Data dan Uji Statistik. Yogyakarta: MediaKom.

Sugiyono.2010.  Statistik Untuk Penelitian. Alfabeta : Bandung.

Uyanto Stanislaus S., Ph.D. 2009. Pedoman Analisis Data dengan SPSS. Edisi 3. Yogyakarta: Graha Ilmu.

Demikian ulasan singkat tentang Pengertian Dan Contoh Kasus Uji Regresi Linear Sederhana Dan Berganda semoga dapat menjadi referensi bagi anda dan jika artikel ini dirasa bermanfaat silahkan bagikan/share artikel ini. Terima kasih telah berkunjung.